La [Semaine de mathématiques 2016->http://eduscol.education.fr/cid59178/semaine-des-mathematiques.html] s’est déroulée au collège du 14 au 18 mars et avait pour thème “maths et sport”. Dans ce cadre, une activité de recherche a germé à partir d’articles lus dans Le Monde et dans “[Le petit vert->http://apmeplorraine.fr/pv/PV125.pdf]”, bulletin de la régionale Lorraine de l’Association des Professeurs de Mathématiques de l’Enseignement Public (APMEP). Un article du Monde du 29/09/15 relatait la découverte, tout à fait récente, d’un quinzième pentagone permettant de paver le plan (comme un puzzle où toutes les pièces auraient la même forme, dans ce cas, pentagonale).
Ce problème du pavage du plan par des pentagones identiques avait agité la communauté mathématique tout au long du XXème. Celle-ci en avait laborieusement dénombré quatorze entre 1918 et 1985. Depuis plus rien ! Et en août 2015, une équipe de trois mathématiciens états-unienne venait d’en découvrir un quinzième. Voici ses caractéristiques géométriques :
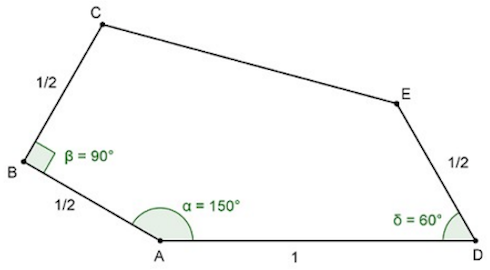
La distance AD étant pris comme unité de longueur, les segments [AB], [BC] et [DE] ont donc pour longueur la moitié de celle de [AD]. Puis, sachant manier un rapporteur, il devient aisé de dessiner, dès la 6ème, ce pentagone. La première idée consistait donc à présenter cette toute récente découverte aux élèves d’une classe et de demander, à chacun d’entre eux, de dessiner un tel pentagone sur une feuille colorée de format A5 pour réaliser un tel pavage (en prenant AD = 10 cm).
Dans la revue “Le petit vert”, on découvrait qu’il existait une deuxième méthode de construction de ce quinzième pentagone. Voir ci-dessous :
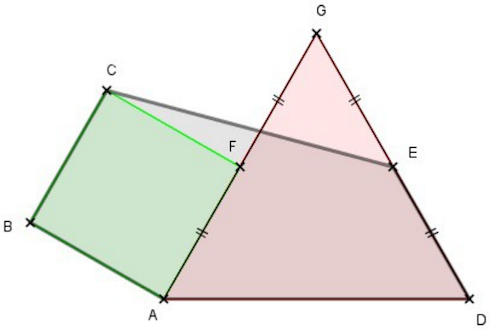
Encore faut-il prouver qu’on obtient bien ainsi le même pentagone. Ce qui nécessite une petite démonstration géométrique accessible dès la 5ème. Dans cette deuxième méthode de construction du pentagone, il faut : -* tracer un segment [AD] dont la longueur sert d’unité de mesure -* construire un triangle équilatéral ADG -* placer les milieux E et F des côtés [DG] et [AG] -* tracer le carré ABCF -* joindre E et C On obtient ainsi le pentagone ABCED recherché. Remarque : ces deux constructions peuvent aisément être réalisées avec le logiciel de géométrie dynamique GeoGebra (téléchargeable gratuitement [ici->https://www.geogebra.org/download]).
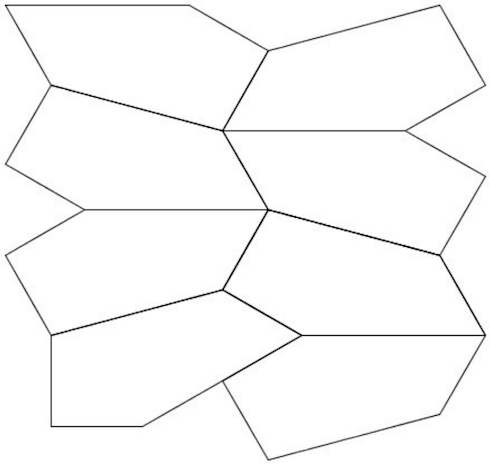
Dernier défi à proposer aux élèves de 4ème et de 3ème : Calculer la longueur exacte du côté [CE], sachant que AD = 1.
Avis aux amateurs de sport cérébral :
le premier élève de 4ème ou 3ème du collège Réeberg Néron qui relèvera ce défi et communiquera sa solution justifiée par courrier électronique à l’auteur de cet article se verra offrir un goûter (1 pain au chocolat + 1 Caresse guyanaise).
